Image correlation basics

Here we synthetically apply a rigid-body transformation to an image and try to measure this transformation using the register image correlation function.

Import modules

import matplotlib.pyplot as plt
import spam.deformation
import spam.DIC
import spam.datasets

Load snow data and create a deformed image

Here we will load the data, define a deformation function and apply it to the data in order to obtain a deformed data set.

We will then visualise the difference between the images – as explained in the Tutorial: Image correlation – Theory.

# Load data
snow = spam.datasets.loadSnow()

# Define transformation to apply
transformation = {'t': [0.0, 3.0, 2.5],
                  'r': [5.0, 0.0, 0.0]}

# Convert this into a deformation function
Phi = spam.deformation.computePhi(transformation)

# Apply this to snow data
snowDeformed = spam.DIC.applyPhi(snow, Phi=Phi)

# Show the difference between the initial and the deformed image.
# Here we used the blue-white-red colourmap "coolwarm"
# which makes 0 white on the condition of the colourmap being symmetric around zero,
# so we force the values with vmin and vmax.
plt.figure()
plt.imshow((snow - snowDeformed)[50], cmap='coolwarm', vmin=-36000, vmax=36000)

<matplotlib.image.AxesImage object at 0x7f11ab1a4130>

Perform correlation

# Now we will use the image correlation function to try
# to measure the Phi between `snow` and `snowDeformed`.
spam.DIC.register(snowDeformed, snow,
                  margin=10,
                  maxIterations=50,
                  deltaPhiMin=0.001,
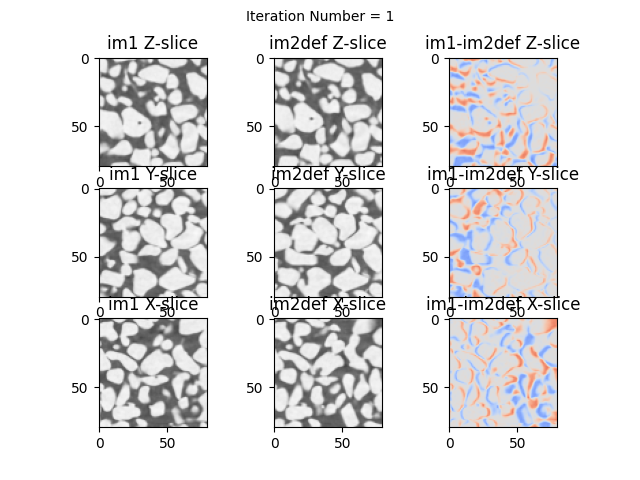
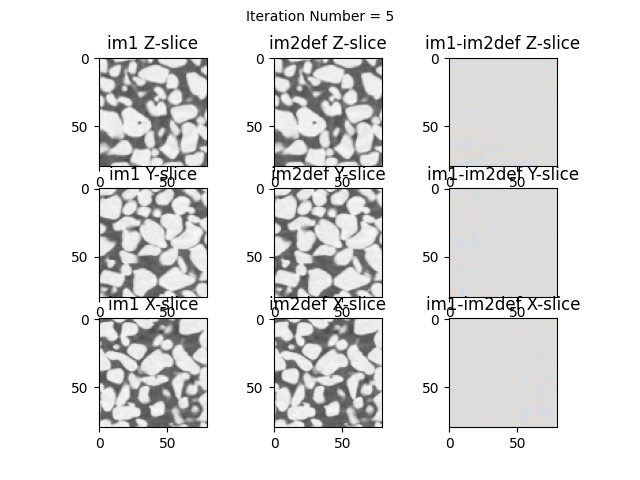
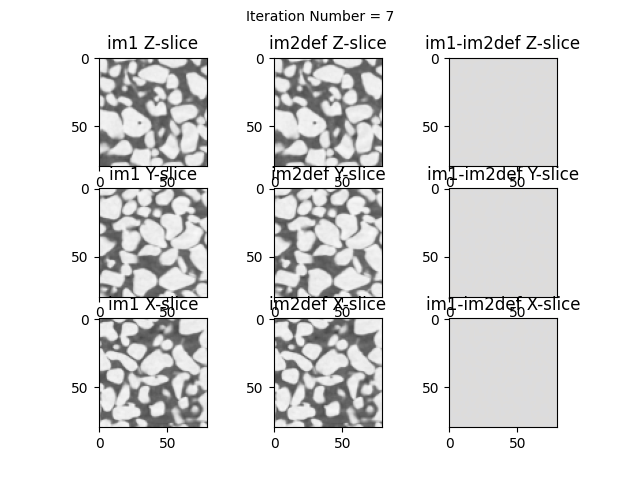
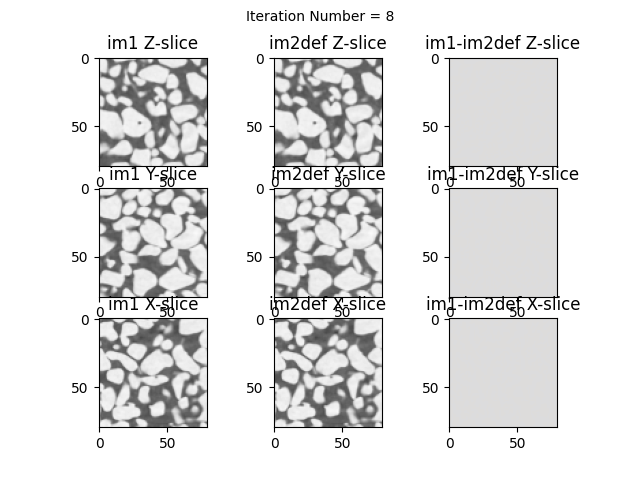
                  verbose=True,                 # Show updates on every iteration
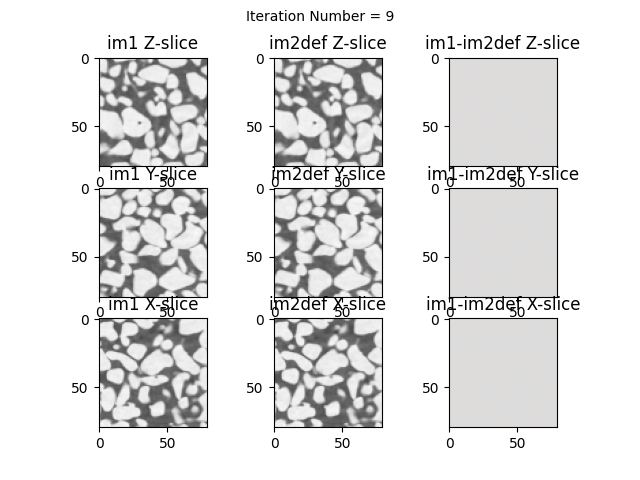
                  imShowProgress=True,           # Show horizontal slice
                  imShowProgressNewFig=True)    # New figure at every iteration

plt.show()

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

Start correlation with Error = 4675.78
    Iteration Number:0  (Elapsed Time: 0:00:00)
    Iteration Number:1   dPhiNorm=0.61465   error=3846.89   t=[0.019 -0.503 -0.352]   r=[-0.292 0.014 0.013]   z=[1.000 1.010 0.991] (Elapsed Time: 0:00:00)
    Iteration Number:2   dPhiNorm=0.59758   error=3263.55   t=[0.021 -0.993 -0.695]   r=[-0.922 -0.003 0.030]   z=[1.000 1.017 0.985] (Elapsed Time: 0:00:00)
    Iteration Number:3   dPhiNorm=0.63556   error=2504.04   t=[0.011 -1.508 -1.068]   r=[-1.818 -0.040 0.051]   z=[1.000 1.022 0.981] (Elapsed Time: 0:00:01)
    Iteration Number:4   dPhiNorm=0.69940   error=1553.99   t=[-0.002 -2.073 -1.479]   r=[-2.904 -0.072 0.069]   z=[1.000 1.023 0.980] (Elapsed Time: 0:00:01)
    Iteration Number:5   dPhiNorm=0.71610   error=572.78   t=[-0.010 -2.664 -1.886]   r=[-3.993 -0.060 0.064]   z=[1.000 1.016 0.986] (Elapsed Time: 0:00:02)
    Iteration Number:6   dPhiNorm=0.54621   error=23.84   t=[-0.004 -3.126 -2.178]   r=[-4.824 -0.012 0.019]   z=[1.000 1.004 0.997] (Elapsed Time: 0:00:02)
    Iteration Number:7   dPhiNorm=0.10894   error=0.46   t=[0.000 -3.217 -2.237]   r=[-5.024 0.002 -0.003]   z=[1.000 1.000 1.000] (Elapsed Time: 0:00:03)
    Iteration Number:8   dPhiNorm=0.01544   error=0.01   t=[-0.000 -3.205 -2.228]   r=[-4.996 -0.000 0.000]   z=[1.000 1.000 1.000] (Elapsed Time: 0:00:03)
    Iteration Number:9   dPhiNorm=0.00238   error=0.00   t=[0.000 -3.207 -2.229]   r=[-5.001 0.000 -0.000]   z=[1.000 1.000 1.000] (Elapsed Time: 0:00:04)
    Iteration Number:10   dPhiNorm=0.00037   error=0.00   t=[0.000 -3.206 -2.229]   r=[-5.000 -0.000 0.000]   z=[1.000 1.000 1.000] (Elapsed Time: 0:00:04)
         -> Converged